qBAS benchmark
qBAS protocol
The qBAS protocol was introduced by M. Benedetti et al. in [1] in 2018. The whitepaper describes the framework Data-Driven Quantum Circuit Learning (DDQCL) which evaluates the performance of quantum computers at learning probabilistic generative models. The data set model to learn for assessing the qBAS score is the Bars and Stripes (BAS) data set. This data set is easy to generate and verify for systems sizes up to hundred of qubits.
Bars and Stripes is a set of images of \(n \times m\) pixels. For a fixed value of \(n\) and \(m\), there are \(N_{BAS(n, m)}=2^n + 2^m -2\) images in the image set. The following picture shows the data set for \(n=m=2\) pixels:
The protocols aims to evaluate the capabilities of quantum computers to uniformely sample bitstring corresponding to each image of this set. Each pixel has a binary color (blue or white) and is associated to a qubit, which states \(\ket{0}\) and \(\ket{1}\) encode the colors. Each image should be sampled with probability \(1/N_{BAS(n, m)}\). The quantum circuit used for the evaluation is a variational circuit composed of \(p\) layers. The implementation of the layer \(U(\theta_i)\) is free but must be parametrized by a single angle \(\theta_i\). Importantly, the number of layers \(p\) and parameters \(\theta_i\) is fixed and do not scale with the size of input instances (we note the list of angles to optimize \(\vec{\theta} = (\theta_1, \theta_2, ..., \theta_p)\)). The gate layout of each layer can be individually optimized to create a circuit template but an overall compilation process optimizing the whole circuit is not authorized.
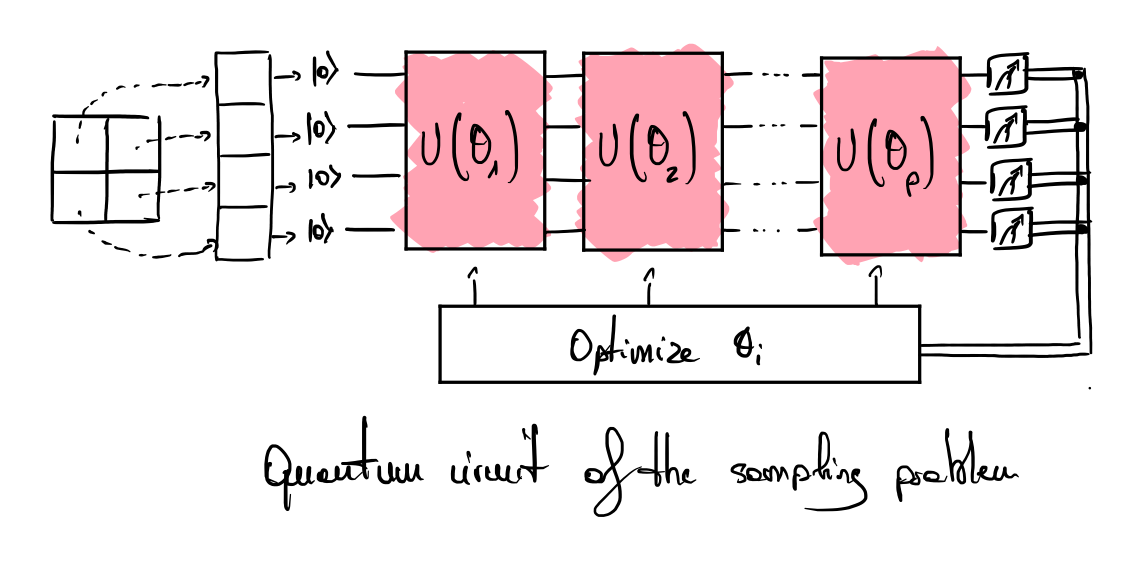
The first step consists in learning the probability distribution of the BAS data set. A sampling composed of \(n_{shots}\) is used to build the empirical probability of observing each bitstring constituting a BAS patterns \(x_i\). The cost function used to optimize the values of the angles \(\vec{\theta}\) is:
\[C \left(\vec{\theta} \right) = \frac{1}{N_{BAS(n, m)}} \sum_{i=1}^{N_{BAS(n, m)}} \ln \left( \max(\epsilon, P_{\vec{\theta}}(x_i)) \right)\]where the \(\epsilon\) is used to avoid cases when \(P_{\vec{\theta}}(x_i) = 0\). The reader might notice that this step do not scale favourably (some clues using other objectives to have a better scaling are given in the suplementary material of [1]).
The second step consists in the estimation of the qBAS-score with the optimized \(\mathbf{\theta}\) parameter. The aim is to evaluate the \(F_1\) score of the parametrized quantum circuit. The \(F_1\) score as the mean between the precision and recall. In this case, the precision is the fraction of sampled states that are effectively BAS patterns. The recall corresponds to the fraction of the number of unique valid patterns \(\lvert \{ x_i \mid P_{\vec{\theta}} (x_i)>0 \} \rvert\) over the total number of unique patterns \(N_{BAS(n, m)}\). To assess this score, setting the number of samples \(n_{shots}\) is very important (otherwise, the recal can be made artificially high). The authors of detail a method to estimate a reasonable number of samplings based on the coupon collector’s problem. We reproduce a table from the artciel that report the number of shots that should be used for different sizes \(n\) and \(m\).
| \((n,m)\) | #qubits | \(N_{BAS(n, m)}\) | \(n_{shots}\) |
|---|---|---|---|
| (2, 2) | 4 | 6 | 15 |
| (2, 3) | 6 | 10 | 30 |
| (3, 3) | 9 | 14 | 46 |
| (4, 4) | 16 | 30 | 120 |
| (7, 7) | 49 | 254 | 1554 |
| (8, 8) | 64 | 510 | 3475 |
| (10, 10) | 100 | 2046 | 16780 |
Configuration of the experiment
- The experimental part does not mention the use of error mitigation methods.
- The structure of the circuit in completely free.
- Each layer of the quantum circuit is used as a template and is fixed.
- The number of shots to assess the qBas score is very important and must be specified.