Quantum LINPACK benchmark

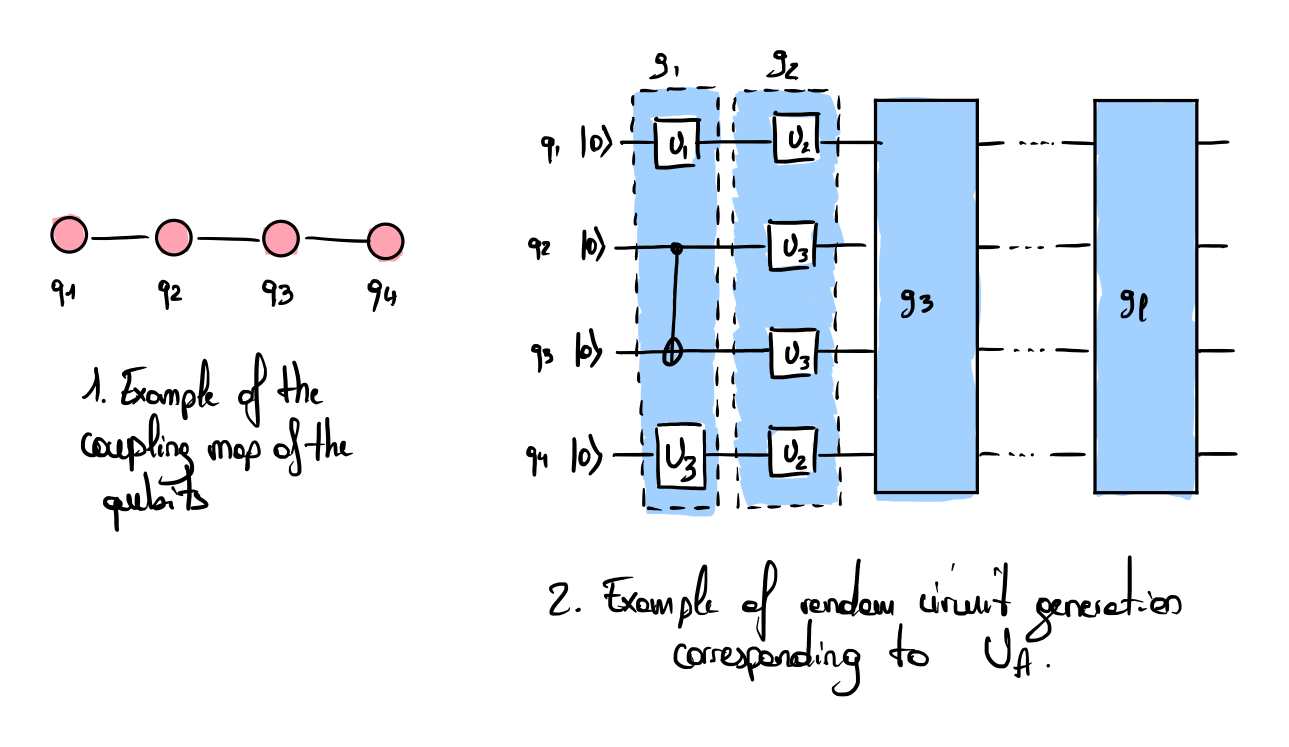
Analogous to the classical LINPACK benchmark [1] [2] used to rank classical supercomputers in the TOP500, Y. Dong et al. [3] propose a protocol to evaluate the performance of quantum computer based on the minimal requirements for solving Quantum Linear System Problems (QLSPs). Given a matrix \(A \in \mathbb{C}^{2^n \times 2^n}\), \(\vec{b} \in \mathbb{C}^{2^n}\) and \(N=2^n\) (where \(n\) is the system size), the objective is to find a solution vector \(\vec{x}\) such that:

\[\begin{bmatrix} A_{11} & A_{12} & ... & A_{1N} \\ A_{21} & A_{22} & ... & A_{2N} \\ ... & ... & ... & ... \\ A_{N1} & A_{N2} & ... & A_{NN} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ ... \\ x_N \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ ... \\ b_N \end{bmatrix}\]

which is equivalent to \(A \vec{x} = \vec{b}\).

Motivation

The primary motivation of Y. Dong et al. is to establish a protocol for assessing the performance of quantum computers in solving Quantum Linear System Problems (QLSPs), similar to the Linpack protocol. The proposed protocol evaluates the quantum device’s capability to prepare a block-encoded matrix, a fundamental subroutine employed by various quantum algorithms designed to address QLSPs.

Protocol details

The protocol is based on the problem of solving a Quantum Linear System Problem (QLSP). Given a matrix \(A \in C^{2^n \times 2^n}\) and a state \(\ket{b} \in C^{2^n}\), the goal is to determine a state \(\ket{x}\) such that \(x \propto A^{-1} \ket{b}\). The solution is encoded in the amplitudes of the state \(\ket{x}\), which can subsequently be used for downstream quantum computation. A significant challenge is the efficient loading of the matrix \(A\) into the quantum computer’s memory, which is often computationally expensive (e.g., using the Linear Combination of Unitary (LCU) method). Instead, the authors of [3] propose a model called the RAndom Circuit Block-Encoded Matrix (RACBEM) that efficiently generates a random circuit \(U_A\) and identifies the corresponding matrix \(A\). The model is extended to Hermitian matrices with the H-RACBEM method.

The random circuit used to implement the unitary \(U_A\) with its corresponding matrix \(A \in \mathbb{C}^{2^n \times 2^n}\) operates on \(n+1\) qubits. The circuit is constructed from a gate set designed to approximate the Haar measure, with two-qubit gates applied according to the quantum chip topology interconnection constraints with defined probability (see Fig 1. for an example of the chip interconnects). As illustrated in Fig. 2, the gate set includes three different single-qubit gate and a single two-qubit gate \(\{U_1, U_2, U_3, CNOT\}\), where each single-qubit \(U_i\) is randomly parameterized. Each circuit layer is composed of a depth-1 layer of 2-qubit and single-qubit gates (see. Fig 2.). Following these layers, a single qubit (the ancilla) is measured to yield the RACBEM. The paper [3] details a second protocol that can be used to generate Hermitian matrices \(A\) called H-RACBEM, which uses an additional ancilla qubit.

Quantum circuit corresponding to the quantum linpack protocol.

The protocol evaluates the probability \(p_{meas}\) of measuring the ancilla qubit in state \(\ket{0}\) (considered as the success probability). This probability is compared to the exact probability computed for ideal circuit \(p_{exact}\) computing the relative error:

\[\epsilon = \frac{|p_{meas}- p_{exact}|}{p_{exact}}\]

Assumptions

The depth of the quantum circuit used to create \(U_A\) should scale as \(poly(n)\) to represent a reliable approximation of the Haar measure.
No compilation method is required as the unitary is generated from the coupling map of the quantum chip.

Limitations

There is no theoretical clue about the hardness of estimating the ancilla’s probability distribution of finishing in state \(\ket{0}\).
As the task only involves two ancilla qubits in the case of H-RACBEM and one in the case of RACBEM, the output distribution of these qubits may be classically spoofed.
The protocol is not hardware agnostic. Hence, comparing the results of different quantum computers can be difficult (especially due to different gate sets and coupling maps).

Implementation

Source code for the generation of the RACBEM: [4]

References

[1]J. J. Dongarra, C. B. Moler, J. R. Bunch, and G. W. Stewart, LINPACK users’ guide. SIAM, 1979.
[2]J. J. Dongarra, P. Luszczek, and A. Petitet, “The LINPACK benchmark: past, present and future,” Concurrency and Computation: practice and experience, vol. 15, no. 9, pp. 803–820, 2003.
[3]Y. Dong and L. Lin, “Random circuit block-encoded matrix and a proposal of quantum LINPACK benchmark,” Physical Review A, vol. 103, no. 6, p. 062412, 2021.
[4]Y. Dong and L. Lin, “RAndom Circuit Block Encoded Matrix (RACBEM).” 2020 [Online]. Available at: https://github.com/qsppack/RACBEM