Binary Randomized Benchmarking (BRB)

Motivations

The Binary Randomized Benchmarking (BRB) protocol was proposed in 2023 by J. Hines et al. in [1]. It initially aims to be more scalable than multi-qubit Clifford RB and Direct RB by removing the stabilizer initialization that requires \(O \left(n^2 / \log(n) \right)\) single and two-qubit gate depth.

Protocol

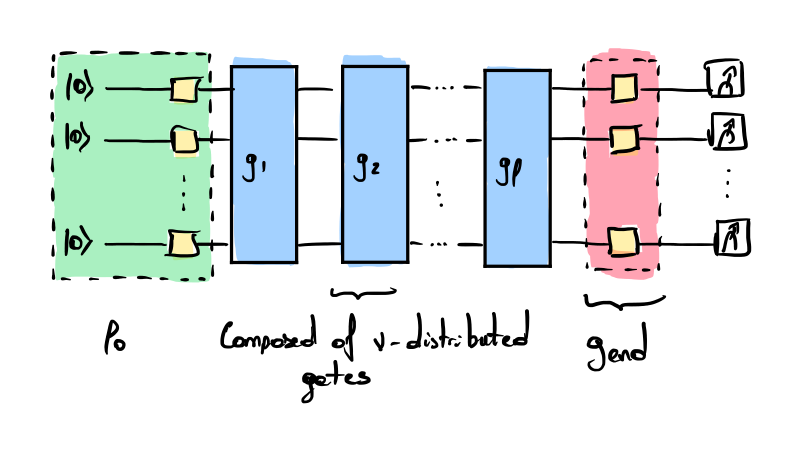
The main difference between BRB and other existing RB protocols is that it does not implement an identity where the whole computation gets cancelled by the \(g_\mathrm{end}\) gate. The initial state \(\rho_0\) is obtained with a layer of single-qubit gates (yellow boxes in the figure) that prepare the \(+1\) eigenstate of a uniformly randomly chosen \(n\)-qubit Pauli Operator. The following sequence of \(g_i\) gates is built according to the user’s probability distribution \(\mu\) (as in the DRB protocol). The last layer \(g_\mathrm{end}\) is a single-qubit gate layer (yellow boxes in the figure) that transforms the quantum state into a tensor product of \(Z\) and \(I\) operators. The success metric is the probability of observing the \(+1\) eigenstate of the tensor product (the output is generally not deterministic, meaning that \(50\%\) of bitstrings are considered successes and others are failure). The success probability permits reconstructing the average error rate of a single layer of random gates \(g_i\).
Interestingly, the authors of BRB explain that this protocol may be better suited for a combination with Simultaneous Randomized Benchmarking than multi-qubit Clifford RB or Direct RB, essentially owing to the the state preparation and measurement layers that are more simply implemented in BRB. They also show that the BRB protocol provides a more precise estimation of the fidelity than the Mirror Randomized Benchmarking protocol.

Assumptions

• This protocol assumes that the noise model is Markovian, meaning that the noise of a gate does not depend on the sequence of previous gates (history-independent).
• The average error of all gates is depolarizing.
• The sampled average fidelity of the random sequences must quickly converge to the average for all possible sequences, as only a small fraction of all possible sequences is being implemented.
• The error should be locally randomized (the basis of the error should be randomized on the \(X\), \(Y\), and \(Z\) axis) and delocalized (see II.B of [1] for mathematical details). These properties ensures that the fidelity will fit an exponential decay.

Limitations

• This protocol can benchmark any set of gates able to generate the Clifford group, but it only scales well for the benchmarking of Clifford gate sets.

Extension

This protocol has been extended to benchmark mid-circuit measurements in [2].

Implementation

An implementation of the BRB protocol is available in the pyGSTi library.

References

1. [1]J. Hines, D. Hothem, R. Blume-Kohout, B. Whaley, and T. Proctor, “Fully Scalable Randomized Benchmarking Without Motion Reversal,” PRX Quantum, vol. 5, no. 3, Aug. 2024, doi: 10.1103/prxquantum.5.030334. [Online]. Available at: http://dx.doi.org/10.1103/PRXQuantum.5.030334
2. [2]D. Hothem, J. Hines, C. Baldwin, D. Gresh, R. Blume-Kohout, and T. Proctor, “Measuring error rates of mid-circuit measurements,” Nature Communications, vol. 16, no. 1, Jul. 2025, doi: 10.1038/s41467-025-60923-x. [Online]. Available at: http://dx.doi.org/10.1038/s41467-025-60923-x