Direct Randomized Benchmarking

Motivations

Direct Randomized Benchmarking (DRB) was proposed by T. Proctor et al. in 2019 [1] to circumvent several limits of the multi-qubit CRB protocol. As the multi-qubit CRB protocol strongly depends on the compilation of the Clifford group into single and two-qubit gates, with circuit depth scaling as \(O(n^2 / \log(n))\) for benchmarking \(n\) qubits, the authors observe that the multi-qubit CRB protocol has not been used to benchmark more than three qubits in practice. DRB is instead intended to directly benchmark the fidelity of native gates in a quantum device, avoiding the costly compilation step. A subsequent study by A. Polloreno et al. developed the theory behind the DRB protocol [2].

Protocol

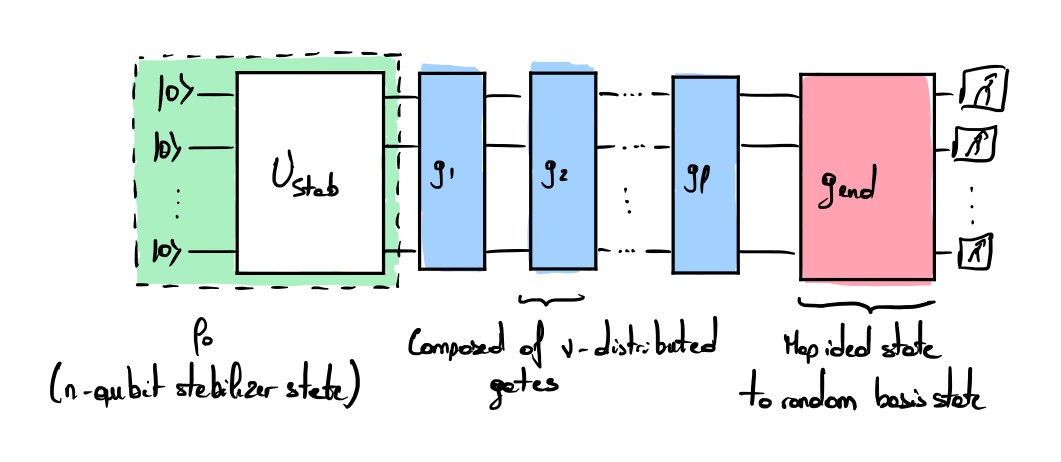
The protocol is used to benchmark \(n\) qubits. At first, a random \(n\)-qubit stabilizer state is created to form the initial state \(\rho_0\) with the unitary \(U_\mathrm{stab}\). Each layer of gate \(g_i\) is drawn from a probability distribution \(\mu\) specified by the user (for example, one could be \(1/4\) probability of having a single CNOT, with the rest consisting of random single-qubit rotations). The only restriction on the distribution \(\mu\) is that it should generate a group of gates that can generate the Clifford group \(\mathbb{C}_n\) (generalized after to unitary-2-design). The ending gate \(g_\mathrm{end}\) projects the quantum state into a random computational basis state so that the final measurement is deterministic (i.e., it measures the sequence’s success or failure). The final measured bitstring \(b\) defines if the computation is a success or failure and requires being computed classically beforehand. The success probability permits reconstructing the average error rate of a single layer of random gates. As the success probability may strongly depend on the distribution \(\mu\) and on the compiler, this information should be reported together carefully.

Assumptions

• This protocol assumes that the noise model is Markovian, meaning that the noise of a gate does not depend on the sequence of previous gates (history-independent).
• The average error of all gates is depolarizing.
• The sampled average fidelity of the random sequences must quickly converge to the average for all possible sequences, as only a small fraction of all possible sequences is being implemented.

Limitations

• Even if the quantum circuit generated by the DRB protocol will be in general shorter than the circuit generated by the multi-qubit CRB protocol, the stabilizer initialization and measurement still require a depth of single and two-qubit gates that scale as \(O \left(n^2 / \log(n) \right)\).
• The protocol is not scalable for all types of gate groups as it requires emulating the output of the quantum circuit to define the bitstring \(b\). However, for groups that only contain Clifford gates, the emulation of the output is efficiently done classically.
• The error rate being measured is slightly overestimated due to the noisy preparation of the \(n\)-qubit stabilizer state (see end of DRB theory section of [1]).

Implementation

An implementation of the DRB protocol is available in the pyGSTi library.

References

1. [1]T. J. Proctor, A. Carignan-Dugas, K. Rudinger, E. Nielsen, R. Blume-Kohout, and K. Young, “Direct randomized benchmarking for multiqubit devices,” Physical review letters, vol. 123, no. 3, p. 030503, 2019.
2. [2]A. M. Polloreno, A. Carignan-Dugas, J. Hines, R. Blume-Kohout, K. Young, and T. Proctor, “A theory of direct randomized benchmarking,” arXiv preprint arXiv:2302.13853, 2023.