Dihedral Randomized Benchmarking

Motivation

Dihedral RB was proposed by A. Carignan-Dugas in 2015 to benchmark other gate sets than the ones implementing the Clifford group [1]. The main motivation of this protocol is to design an efficient method to benchmark other gate sets than the Clifford group to evaluate the error rate of gates required for universal quantum computing (such as the T-Gate).

Protocol

The Dihedral RB protocol evaluates the average fidelity of a single-qubit unitary group of gates called the dihedral group. For a fixed \(j\), the dihedral group \(\mathcal{D}_j\) comprises a parameterized rotation gate \(R_j(z_i) = e^{i \pi z_i/j Z}\) (where \(Z\) corresponds to the Pauli-Z gate) and a Pauli-\(X\) gate.
The protocol starts by fixing \(j\). In the initial paper, the authors mainly use \(j=4\) and \(j=8\). The experiment is done for different sequence lengths \(l\). For each sequence length, two arrays of integers are uniformly and randomly generated: \(\mathbf{z} = (z_1, z_2, ..., z_l)\) with \(z_i \in \{0, 1, 2 ..., j-1\}\) and \(\mathbf{x} = (x_1, x_2, ..., x_l)\) with \(x_i \in \{0, 1\}\). The system is prepared either in state \(\ket{0}\) or in state \(\ket{+}\). Each gate of the sequence \(g_i\) is composed of the \(R_j(z_i)\) gate and the \(X^{x_i}\) gate. The last quantum gate \(g_{end}\) is used to invert the preceding sequence of quantum gates. The final measurement is done such that an ideal evolution should give a \(+1\) outcome of the POVM. This success probability is then used to fit the decay function and extract the average gate fidelity. The parameters \(b_1\) and \(b_2\) are used to ease the fitting of the decaying function (see [1] for details).

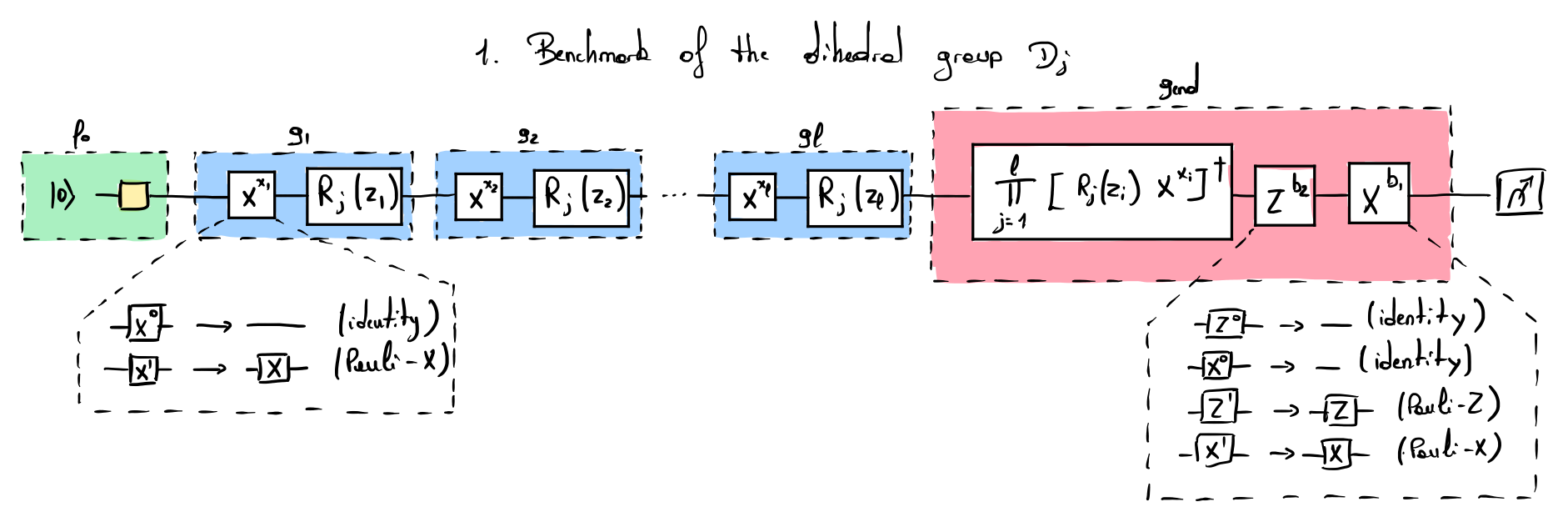
Focusing on \(\mathcal{D}_4\) and \(\mathcal{D}_8\) permits benchmarking the fidelity of the T gate. Indeed, the group \(\mathcal{D}_4\) is only generated from Clifford gates (phase and Pauli-X). \(\mathcal{D}_8\) can be implemented using \(\mathcal{D}_4\) and adding the T gate. The difference of average fidelity between \(\mathcal{D}_4\) and \(\mathcal{D}_8\) permits to estimate the average fidelity of the T gate.
At first, the average fidelity of \(\mathcal{D}_4\) is established using the circuit in Fig. 1. The fidelity of the T gate is then evaluated by combining the dihedral benchmarking method with the interleaved RB protocol (implemented by the circuit shown in Fig. 2). It has the effect of adding a T gate (\(R_8(1)\)) at the end of each gate \(g_i\). The average fidelity of the T gate can then be estimated by comparing the result of the interleaved experiment to the experiment done for \(\mathcal{D}_4\). The estimated value is tight if the gates from \(D_4\) have much higher fidelity than the T gate, which is argued by the author to be the regime of interest.

In this example, measurements are done along the \(z\)-axis but the protocol can be extended to characterize other single-qubit rotations.

Assumptions

• This protocol assumes that the noise model is Markovian, meaning that the noise of a gate does not depend on the sequence of previous gates (history-independent).
• The method used to estimate the fidelity of the T gate is only valid if the quality of the Clifford gates is significantly greater than the fidelity of the T gate.

Limitations

• The average fidelity of the T gate is estimated from an approximation, and its bound is tight only when the fidelity of Clifford gates is much higher than that of the T gate (see numerical simulation part of [1]).

Extension

This protocol has been extended to multiple qubits in [2] by A. Cross et al.

Implementation

Part of the extended protocol is available in the Qiskit SDK.

References

1. [1]A. Carignan-Dugas, J. J. Wallman, and J. Emerson, “Characterizing universal gate sets via dihedral benchmarking,” Physical Review A, vol. 92, no. 6, p. 060302, 2015.
2. [2]A. W. Cross, E. Magesan, L. S. Bishop, J. A. Smolin, and J. M. Gambetta, “Scalable randomised benchmarking of non-Clifford gates,” npj Quantum Information, vol. 2, no. 1, pp. 1–5, 2016.