Energy relaxation time \(T1\)
Motivation
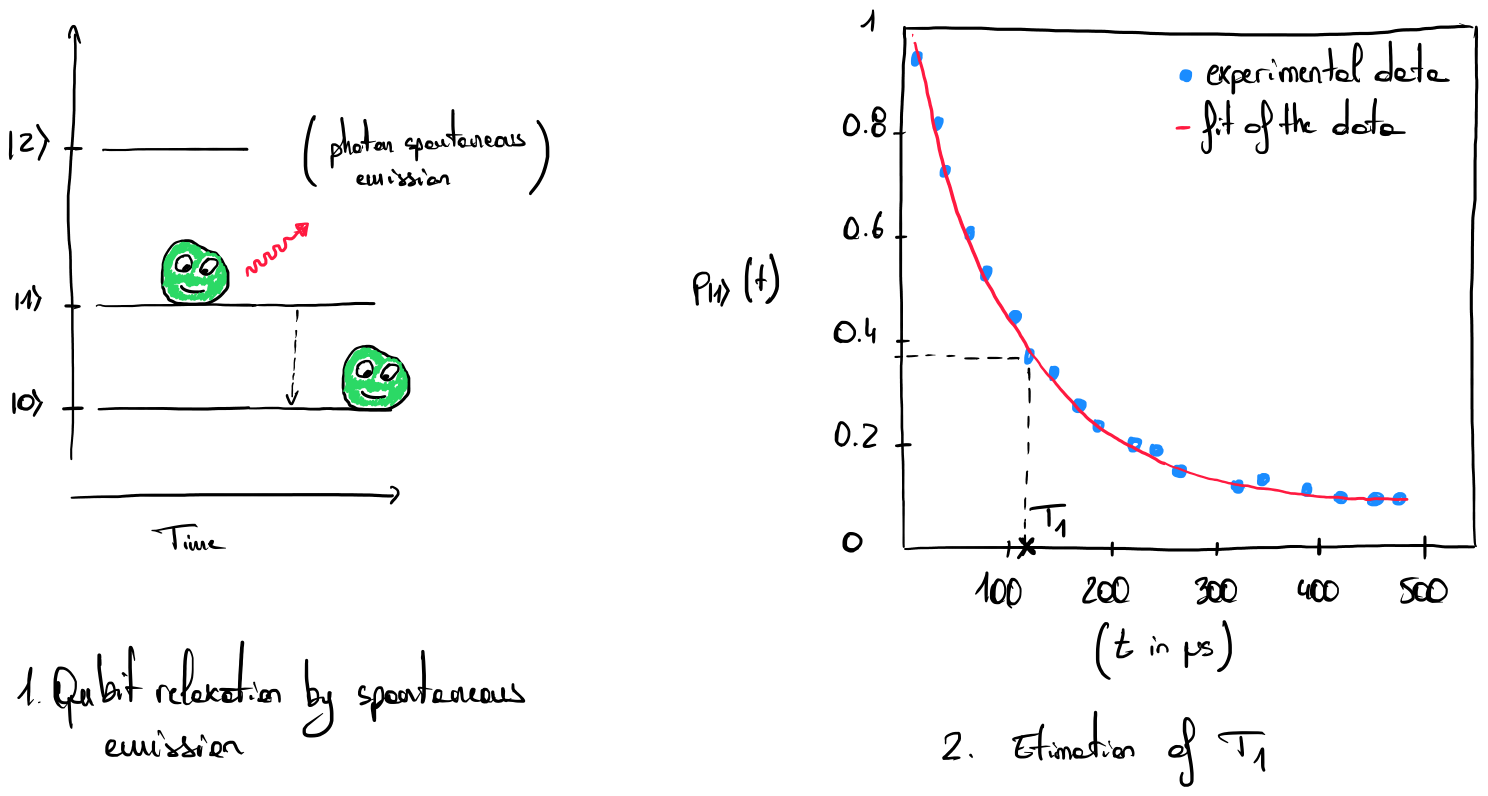
A qubit prepared in an excited state \(\ket{1}\) may naturally and spontaneously deexcite to its ground state \(\ket{0}\). This process, called spontaneous emission, can be characterized by measuring the time \(T_1\), which defines the timescale at which the qubit turns from an excited state \(\ket{1}\) to the ground state \(\ket{0}\) (see Fig. 1 for a simplified representation of an energy diagram and the impact of energy relaxation).
Protocol
The protocol used to measure \(T_1\) starts by initializing the qubit in the excited state \(\ket{1}\). It can be done by preparing the qubit in state \(\ket{0}\), then applying an \(X\) gate on this qubit. Then, the qubit is left idle for some time \(t\) and is measured in the \(Z\)-basis. This experiment is repeated several times to extract the probability of the outcome confidently. These data are then used to fit the exponential decay function that describes the probability of being prepared in state \(\ket{1}\) and being measured in state \(\ket{1}\) with respect to time:
\[p_{\ket{1}}(t) = e^{-t/T_1}\]The decay rate \(\Gamma_1\) is related to \(T_1\) by the relation:
\[T_1 = \frac{1}{\Gamma_1}\]\(T_1\) represents the value in the abscissa when \(p_{\ket{1}}(t)=1/e\) (see Fig. 2).
Assumptions
In the protocol description, it is assumed that the higher-energy state is the excited state \(\ket{1}\).
Limitations
- Some uncertainty can arise from the \(T_1\) measurement if the preparation, the \(X\) gate, and measurement operations are not well calibrated.
- Measuring \(T_1\) for quantum annealers can be misleading, essentially because quantum annealers can operate successfully beyond this timescale (see [1] and [2] for interesting discussions on this subject).
Implementation Examples
A tutorial for measuring \(T_1\) is available in the QCMet software repository.
Another tutorial can be found on the qiskit-community github.
References
- [1]D. Lall et al., “A review and collection of metrics and benchmarks for quantum computers: definitions, methodologies and software,” arXiv preprint arXiv:2502.06717, 2025.
- [2]N. G. Dickson et al., “Thermally assisted quantum annealing of a 16-qubit problem,” Nature Communications, vol. 4, no. 1, May 2013, doi: 10.1038/ncomms2920. [Online]. Available at: http://dx.doi.org/10.1038/ncomms2920
