Clifford Volume Benchmark

Motivation

The main motivation for the Clifford Volume (CLV) is to define a scalable and hardware-agnostic metric, reusing the idea of the well-known quantum volume. A quantum computer with a Clifford Volume (CLV) equal to \(n\) should be able to execute a single \(n\)-qubit Clifford unitary reliably.

Protocol

The Clifford Volume (CLV) [1] is a scalable benchmark, in the sense that it can be used to evaluate quantum computers beyond 50 qubits, which is not possible when using the Quantum Volume, as it requires a classical computation that grows exponentially with the number of qubits. The protocol consists of preparing a stabilizer state from an \(n\)-qubit Clifford gate and then measuring the expectation value of randomly picked \(n\)-qubit Pauli operators. The aim is to determine if the sampling is sufficient to distinguish whether the \(n\)-qubit Pauli operator is part of the generators associated with the \(n\)-qubit Clifford gate or if this operator is outside the generator group.

Clifford Volume circuit

The following steps define how to generate a circuit used for assessing the CLV of a quantum computer:

• Choose a number \(n\) as the width of the circuit (i.e., the number of qubits in the circuit).
• Initialize all the qubits in state \(\ket{0}\) (green part of the figure).
• Generate a random \(n\)-qubit Clifford unitary (blue part of the figure) and apply the corresponding gate sequence to the qubits. In general, implementing a \(n\)-qubit Clifford gate imply a circuit depth of \(O(n^2/\log(n))\) gates (some extras could be involved if the qubits of the chip are not fully interconnected). This sequence might be highly optimized.
• Measure a randomly chosen Pauli operator. It can be done using an extra layer of gates to produce the corresponding eigenstate of the \(\sigma^z\) operator, if the quantum computer is only able to measure in the z-basis. This step is represented in red in the figure.

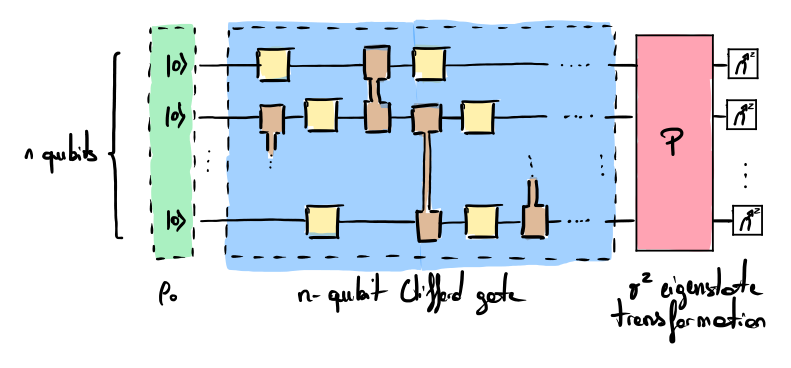
The experiment is repeated many times for each \(n\)-qubit Clifford unitary, measuring different random Pauli operators. More specifically, for each Clifford gate, two sets of operators are created: one that contains generators associated with the Clifford unitary noted \(S\) (with \(\left<S_i\right>=1\) in ideal simulations) and one that includes operators that are outside the generator group \(\mathcal{D}\) (with \(\left<D_i\right>=0\) in ideal simulations). For each group, it is then checked that:

where \(\sigma_i\) denotes the standard deviation of the expectation value of the operator \(\mathcal{S}_i\) or \(\mathcal{D}_i\). Another criterion is used to verify the behavior of the quantum computer in the average case for every Clifford gate (see eqn 7 and 8 in [1]).

A Clifford volume \(n\) is validated if the criteria explained above are all correct. In the European Quantum Computing Benchmark suite [2], the same authors advise randomly generating \(4\) different Clifford gates, with \(8\) operators randomly picked: \(4\) from the generator group \(S\) and \(4\) from outside of the generator group \(D\). The number of shots per circuit is at least set to \(512\).

Assumptions

• The circuit compiler may use all possible tricks to improve the mapping of the quantum circuit, which can lead to significant extra processing time.
• The quantum computer should honestly attempt to implement the \(n\)-qubit Clifford gate and not choose an implementation far from the initial circuit model (i.e., the approximation error should be limited).
• The output of the quantum circuit should not be post-processed to improve the results (i.e., error mitigation methods are prohibited).
• The Clifford unitary and measurement operators should be randomly generated once without replacement.

Limitations

• The CLV assesses only a limited subset of best-quality qubits within a quantum processor and does not provide a comprehensive measure of the overall fidelity or performance of quantum operations across the entire chip.
• Due to the optimized compilation step allowed by the protocol, results obtained by the manufacturer on their quantum chip may often be hard to reproduce due to advanced and proprietary optimization settings (same issue as with the quantum volume).
• The initial protocol recommends a very small number of distinct Clifford unitaries and measurement operators to validate a Clifford volume of size \(n\). Due to this small number, this experiment might be easily spoofed and require trust (for example, if it’s evaluated directly by manufacturers themselves).

Implementations

The implementation of the authors of the original papers is available here. This protocols has been included in the European Quantum Computing Benchmark suite.

References

1. [1]A. Portik, O. Kálmán, T. Monz, and Z. Zimborás, “Clifford Volume and Free Fermion Volume: Complementary Scalable Benchmarks for Quantum Computers,” arXiv preprint arXiv:2512.19413, 2025.
2. [2]Z. Zimborás et al., “The EU Quantum Flagship’s Key Performance Indicators for Quantum Computing,” arXiv preprint arXiv:2512.19653, 2025.