Quantum Volume Benchmark
Benchmarking results
List of acronyms
CE: Constructor Evaluation (checked if the evaluation is done by the chip manufacturer)
SP: Scientific paper (checked if a scientific paper explain the results)
#Circ: number of circuits used for the evaluation
For clarity the Quantum Volume is expressed in a logarithmic basis.
The reader should consider with caution the results that are not supported with a scientific paper (SP column without a check).
| Ref | Company | Year | CE | SP | #Circ | Shots | CPU / QPU | Technology | Chip qubits | \(\log_2(QV)\) | Comment |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [2] [3] | AQT | 2024/08 | x | 870 | IBEX Q1 | Trapped-ions | 12 | 7 | protocol [4] | ||
| [2] [5] | AQT | 2024/08 | x | 870 | MARMOT | Trapped-ions | 20 | 7 | protocol [4] | ||
| [6] | IBM | 2020/07 | x | x | Johannesburg | Superconducting | 20 | 5 | initial protocol [1] | ||
| [7] | IBM | 2020/09 | x | x | Montreal | Superconducting | 27 | 6 | initial protocol [1] | ||
| [8] | IBM | 2022/12 | x | sherbrooke (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | sherbrooke (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | brisbane (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | brisbane (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | osaka (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | osaka (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | kyoto (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | kyoto (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | Quebec (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | kawasaki (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | rensselaer (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | kyiv (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | cleveland (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | nazca (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2022/12 | x | cusco (Eagle r3) | Superconducting | 127 | 7 | initial protocol [1] | |||
| [8] | IBM | 2023/12 | x | torino (Heron r1) | Superconducting | 133 | 9 | initial protocol [1] | |||
| [9] | IBM | 2025/09 | x | pittsburgh (Heron r3) | Superconducting | 156 | 10 | protocol [4] | |||
| [10] | IonQ | 2022/03 | x | 1000 | 20 | Harmony | Trapped-ions | 11 | 3 | initial protocol [1] | |
| [10] | OQC | 2022/03 | x | 1000 | 20 | Lucy | Superconducting | 8 | 0 | initial protocol [1] | |
| [11] | Rigetti | 2020/01 | x | Aspen-4 | Superconducting | 16 | 3 | initial protocol [1] | |||
| [10] | Rigetti | 2022/03 | x | 1000 | 20 | Aspen-11 | Superconducting | 38 | 2 | initial protocol [1] | |
| [10] | Rigetti | 2022/03 | x | 1000 | 20 | Aspen-M-1 | Superconducting | 80 | 3 | initial protocol [1] | |
| [10] | Quantinuum | 2022/03 | x | 1000 | 20 | H1-2 | Trapped-ions | 12 | 9 | initial protocol [1] | |
| [12] [13] | Quantinuum | 2020/06 | x | x | 400 | 100 | H0 | Trapped-ions | 6 | initial protocol [1] | |
| [14] [13] | Quantinuum | 2020/09 | x | H1-1 | Trapped-ions | 7 | initial protocol [1] | ||||
| [13] | Quantinuum | 2021/03 | x | H1-1 | Trapped-ions | 9 | initial protocol [1] | ||||
| [13] | Quantinuum | 2021/07 | x | H1-1 | Trapped-ions | 10 | initial protocol [1] | ||||
| [15] [13] | Quantinuum | 2021/09 | x | 2000 | 5 | H1-2 | Trapped-ions | 11 | initial protocol [1] | ||
| [16] [13] | Quantinuum | 2022/04 | x | 200 | 100 | H1-2 | Trapped-ions | 12 | initial protocol [1] | ||
| [17] [13] | Quantinuum | 2022/09 | x | 220 | 90 | H1-1 | Trapped-ions | 13 | protocol [4] | ||
| [13] | Quantinuum | 2021/01 | x | H1-1 | Trapped-ions | 14 | protocol [4] | ||||
| [18] [13] | Quantinuum | 2021/01 | x | 100 | 200 | H1-1 | Trapped-ions | 15 | protocol [4] | ||
| [13] | Quantinuum | 2023/04 | x | H2-1 | Trapped-ions | 15 | protocol [4] | ||||
| [19] [13] | Quantinuum | 2023/04 | x | x | 200 | 100 | H2-1 | Trapped-ions | 16 | protocol [4] | |
| [13] | Quantinuum | 2023/03 | x | H1-1 | Trapped-ions | 16 | protocol [4] | ||||
| [16] [13] | Quantinuum | 2023/05 | x | H1-1 | Trapped-ions | 17 | protocol [4] | ||||
| [16] [13] | Quantinuum | 2023/05 | x | H1-1 | Trapped-ions | 18 | protocol [4] | ||||
| [16] [13] | Quantinuum | 2023/06 | x | H1-1 | Trapped-ions | 19 | protocol [4] | ||||
| [13] | Quantinuum | 2023/10 | x | H1-2 | Trapped-ions | 15 | protocol [4] | ||||
| [13] | Quantinuum | 2024/04 | x | H1-1 | Trapped-ions | 20 | protocol [4] | ||||
| [13] | Quantinuum | 2024/05 | x | H2-1 | Trapped-ions | 18 | protocol [4] | ||||
| [20] | Quantinuum | 2024/08 | x | H2-1 | Trapped-ions | 21 | protocol [4] | ||||
| [21] | Quantinuum | 2025/05 | x | H2-1 | Trapped-ions | 23 | protocol [4] | ||||
| [22] | Quantinuum | 2025/09 | x | H2-2 | Trapped-ions | 56 | 25 | protocol [4] | |||
| [23] | IQM | 2024/08 | x | x | Garnet | Superconducting | 20 | 5 | initial protocol [1] | ||
| [24] | QuTech | 2023/08 | x | 100 | 100 | Starmon-5 | Superconducting | 5 | 2 | initial protocol [1] | |
| [25] | University | 2024/12 | x | x | NV Center | 3 | 3 | initial protocol [1] QV simulated from noise model |
Motivation
The main motivation for the Quantum Volume (QV) is to define a pragmatic way to evaluate and compare progress for near-term quantum computing. The QV is a single number figure of merit used to evaluate universal gate-based quantum computers. A quantum computer with a Quantum Volume (QV) of size \(n\) is able to reliably execute a quantum circuit with at most \(n\) qubits with maximum gate depth \(n\) [1].
Protocol
The Quantum Volume (QV) [26] [1] is a benchmarking protocol evaluating the ability of gate-based quantum computers to run quantum circuits reliably. This protocol gathers the maximum circuit width and depth that a quantum computer can successfully implement in a single metric number. A quantum computer has to successfully solve the Heavy Output Generation (HOG) problem [27] of size \(n\) to validate a quantum volume of size \(2^n\). Many criteria may impact the value of the quantum volume: gate fidelity, coherence time, chip topology, and the efficiency of the transpilation method.
Heavy Output Generation problem
The HOG problem is a sampling problem [27] considered hard for classical computers and constitutes a pass/fail test for quantum computers.
The problem is stated as:
Let \(Q\) be a random circuit drawn from a suitable ensemble acting on \(n\) qubits. The quantum state after executing the circuit is denoted \(\ket{\psi}\). Each possible output state \(x \in \{0, 1\}^n\) is measured with probability \(|\left<x|\psi\right>|^2\).
The set of output states with a probability greater than the median constitutes the heavy set of outputs associated with the quantum circuit \(Q\).
Quantum Volume circuit
The following steps define how to generate quantum volume circuits:
- Choose a number \(n\) as the width of the circuit (i.e., the number of qubits in the circuit).
- Set the number of layers of the quantum circuit to \(n\).
- Generate a model circuit composed of \(n\) layers. Each layer comprises a random permutation (random relabelling) of qubits \(\pi\) and a random unitary sampled from \(SU(4)\). The permutation step is challenging for quantum chips with limited interconnections because it requires many swapping gates. The \(SU(4)\) gates can be decomposed into three CNOT gates and seven single-qubit rotation gates [28].
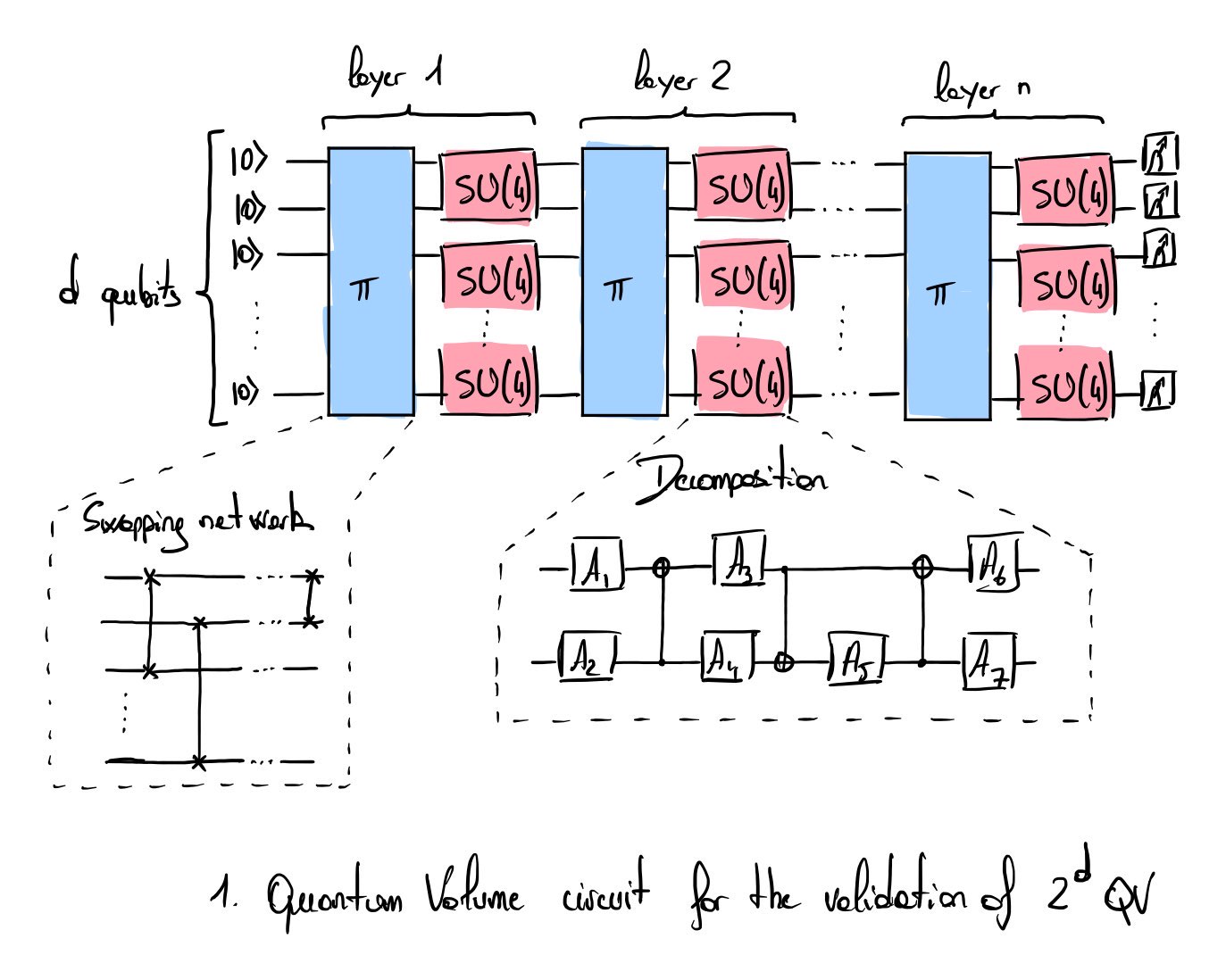
This circuit is then used as input for the sampling task associated with the Heavy Output Generation (HOG) problem. If the quantum computer samples the right distribution (simulated classically), it validates the corresponding quantum volume score of \(2^n\). The confidence interval for this evaluation is set to two-sigma (\(97.73 \%\)).
Assumptions
- The circuit compiler may use all the possible tricks to improve the mapping of the quantum circuit, which can lead to possibly high extra-processing time. In [4], the authors show that the compilation has a strong impact on small quantum volumes (\(< 10\)) as it can reduce the number of 2-qubit gates.
- The quantum computer should honestly attempt to solve the HOG problem and not choose an implementation far from the initial model of the circuit (i.e., the approximation error should be limited).
Limitations
- Quantum volume assesses only a limited subset of best-quality qubits within a quantum processor and does not provide a comprehensive measure of the overall fidelity or performance of quantum operations across the entire chip.
- Previous experiments [10] have shown that the Quantum Volume measured by quantum chip manufacturers is often hard to reproduce due to advanced optimization settings (compilation optimization and approximation of quantum gates) used to boost the performance of the quantum computer for passing this test.
Protocol Variations
In [4], the authors argue that the confidence interval built in the initial test [1] is more restrictive than necessary. They propose a new tighter confidence interval that still covers the initial requirement of \(97.73\%\) (using bootstrapping).
In [29], the authors extend the quantum volume protocol to verify the output sampling distribution for large experiments. This method uses parity tests to determine the heavy output probability distribution efficiently.
Implementations
Several implementations of the Quantum Volume are available on GitHub:
- The implementation of IBM using Qiskit is available here.
- A tutorial implementation from the QCMet software repository [30] is available here.
- Another tutorial implementation from Pennylane is available here.
References
- [1]A. W. Cross, L. S. Bishop, S. Sheldon, P. D. Nation, and J. M. Gambetta, “Validating quantum computers using randomized model circuits,” Physical Review A, vol. 100, no. 3, p. 032328, 2019.
- [2]A. Frisch et al., “Trapped-Ion Quantum Computing,” in Quantum Software, Springer Nature Switzerland, 2024, pp. 251–283 [Online]. Available at: http://dx.doi.org/10.1007/978-3-031-64136-7_10
- [3]AQT, “IBEX Q1 Our quantum computer system that executes your quantum circuits via cloud access.” 2024 [Online]. Available at: https://www.aqt.eu/products/ibex-q1/
- [4]C. H. Baldwin, K. Mayer, N. C. Brown, C. Ryan-Anderson, and D. Hayes, “Re-examining the quantum volume test: Ideal distributions, compiler optimizations, confidence intervals, and scalable resource estimations,” Quantum, vol. 6, p. 707, 2022.
- [5]AQT, “MARMOT The first commercial 19-inch rack-mounted quantum computer.” 2024 [Online]. Available at: https://www.aqt.eu/products/marmot/
- [6]N. Sundaresan, I. Lauer, E. Pritchett, E. Magesan, P. Jurcevic, and J. M. Gambetta, “Reducing unitary and spectator errors in cross resonance with optimized rotary echoes,” PRX Quantum, vol. 1, no. 2, p. 020318, 2020.
- [7]P. Jurcevic et al., “Demonstration of quantum volume 64 on a superconducting quantum computing system,” Quantum Science and Technology, vol. 6, no. 2, p. 025020, 2021.
- [8]IBM, “Processor types.” 2024 [Online]. Available at: https://docs.quantum.ibm.com/run/processor-types
- [9]IBM, “IBM pittsburgh announcement.” 2025 [Online]. Available at: https://www.linkedin.com/posts/jay-gambetta-a274753a_following-up-on-an-earlier-post-https-activity-7364268815720824834-aZ0k/
- [10]E. Pelofske, A. Bärtschi, and S. Eidenbenz, “Quantum volume in practice: What users can expect from nisq devices,” IEEE Transactions on Quantum Engineering, vol. 3, pp. 1–19, 2022.
- [11]P. J. Karalekas, N. A. Tezak, E. C. Peterson, C. A. Ryan, M. P. Da Silva, and R. S. Smith, “A quantum-classical cloud platform optimized for variational hybrid algorithms,” Quantum Science and Technology, vol. 5, no. 2, p. 024003, 2020.
- [12]J. M. Pino et al., “Demonstration of the trapped-ion quantum CCD computer architecture,” Nature, vol. 592, no. 7853, pp. 209–213, 2021.
- [13]Quantinuum, “Quantuum Hardware Quantum Volume Data.” 2024 [Online]. Available at: https://github.com/CQCL/quantinuum-hardware-quantum-volume
- [14]Honeywell, “Achieving quantum volume 128 on the Honeywell Quantum Computer.” 2020 [Online]. Available at: https://www.honeywell.com/us/en/news/2020/09/achieving-quantum-volume-128-on-the-honeywell-quantum-computer
- [15]Quantinuum, “Demonstrating Benefits of Quantum Upgradable Design Strategy: System Model H1-2 Frist to Prove 2048 Quantum Volume.” 2021 [Online]. Available at: https://www.quantinuum.com/news/demonstrating-benefits-of-quantum-upgradable-design-strategy-system-model-h1-2-first-to-prove-2-048-quantum-volume
- [16]Quantinuum, “Quantinuum Announces Quantum Volume 4096 Achievement.” 2022 [Online]. Available at: https://www.quantinuum.com/news/quantinuum-announces-quantum-volume-4096-achievement
- [17]Quantinuum, “Quantinuum Sets New Record with Highest Ever Quantum Volume.” 2022 [Online]. Available at: https://www.quantinuum.com/news/quantinuum-sets-new-record-with-highest-ever-quantum-volume
- [18]Quantinuum, “Quantum Volume reaches 5 digits for the first time: 5 perspectives on what it means for quantum computing.” 2023 [Online]. Available at: https://www.quantinuum.com/news/quantum-volume-reaches-5-digits-for-the-first-time-5-perspectives-on-what-it-means-for-quantum-computing
- [19]S. A. Moses et al., “A race-track trapped-ion quantum processor,” Physical Review X, vol. 13, no. 4, p. 041052, 2023.
- [20]Quantinuum, “System Model H2.” 2024 [Online]. Available at: https://www.quantinuum.com/products-solutions/quantinuum-systems/system-model-h2#h2-resources
- [21]Quantinuum, “Quantinuum Dominates the Quantum Landscape: New World-Record in Quantum Volume.” 2025 [Online]. Available at: https://www.quantinuum.com/blog/quantum-volume-milestone
- [22]Quantinuum, “System Benchmarks.” 2025 [Online]. Available at: https://docs.quantinuum.com/systems/user_guide/hardware_user_guide/benchmarks/system_benchmarks.html
- [23]L. Abdurakhimov et al., “Technology and Performance Benchmarks of IQM’s 20-Qubit Quantum Computer,” arXiv preprint arXiv:2408.12433, 2024.
- [24]W. van der Schoot, R. Wezeman, P. T. Eendebak, N. M. P. Neumann, and F. Phillipson, “Evaluating three levels of quantum metrics on quantum-inspire hardware,” arXiv preprint arXiv:2310.01120, 2023.
- [25]T. Jaeger et al., “Modeling Quantum Volume Using Randomized Benchmarking of Room-Temperature NV Center Quantum Registers,” arXiv preprint arXiv:2412.12959, 2024.
- [26]L. S. Bishop, S. Bravyi, A. Cross, J. M. Gambetta, and J. Smolin, “Quantum volume,” Quantum Volume. Technical Report, 2017.
- [27]S. Aaronson and L. Chen, “Complexity-theoretic foundations of quantum supremacy experiments,” arXiv preprint arXiv:1612.05903, 2016.
- [28]F. Vatan and C. Williams, “Optimal quantum circuits for general two-qubit gates,” Physical Review A—Atomic, Molecular, and Optical Physics, vol. 69, no. 3, p. 032315, 2004.
- [29]R. Bistroń, M. Rudziński, R. Kukulski, and K. Życzkowski, “Benchmarking quantum devices beyond classical capabilities,” arXiv preprint arXiv:2502.02575, 2025.
- [30]D. Lall et al., “A review and collection of metrics and benchmarks for quantum computers: definitions, methodologies and software,” arXiv preprint arXiv:2502.06717, 2025.
