Quantum Unitary Evolution Score (QUES)
Motivation
Y. Dong et al. introduced the QUES protocol in [1]. Their main motivation is to provide a method to benchmark the performance of gate-based quantum computers to run a time-independent Hamiltonian simulation. It is done by implementing a minimalist version of the Quantum Singular Value Transformation (QSVT) algorithm. This approach is scalable, and the score can be calculated beyond the classical verifiable regime.
Protocol details
The protocol defines a QSVT circuit of minimum size called minimal QSVT (mQSVT) consisting of \(n\) qubits and a single ancilla qubit. The circuit comprises \(l\) layers, each involving the application of a unitary \(U_A\) and its adjoint \(U_A^\dagger\), interleaved with \(R_z\) gates. These rotations are parameterized by a sequence of phase angles \((\phi_1, \phi_2, ... \phi_{2l +1})\). The quantum circuit associated with this protocol is illustrated in Fig. 1.
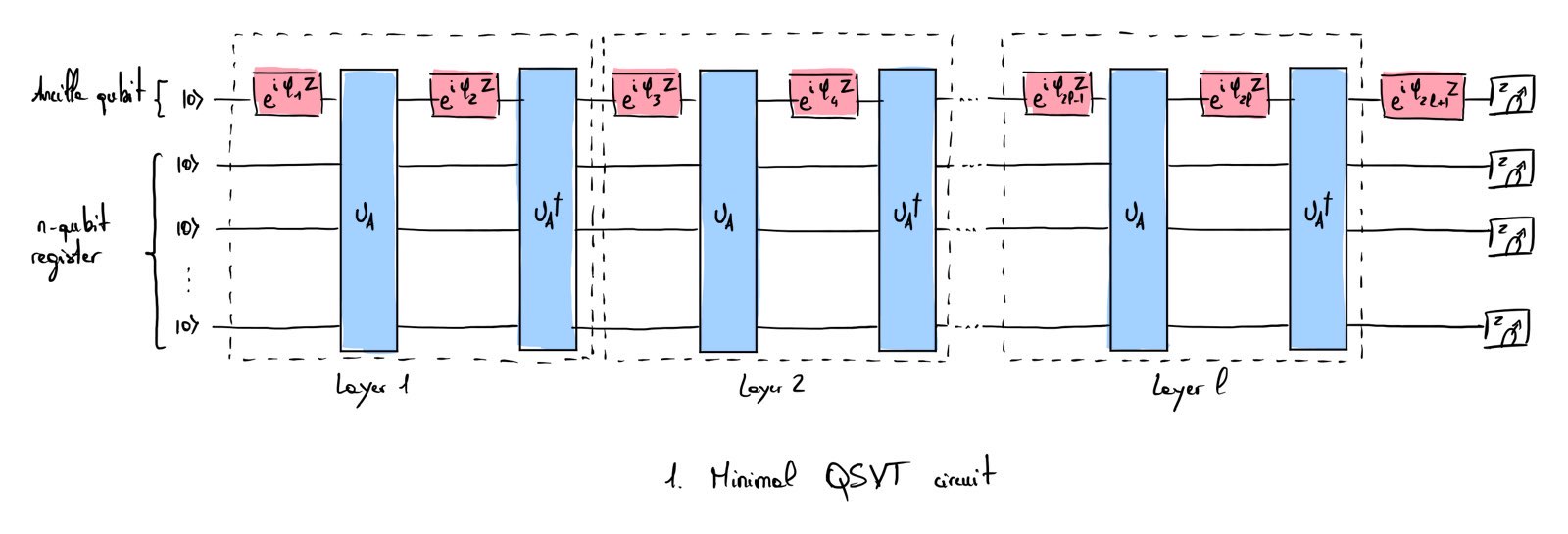
For a quantum circuit composed of \(n+1\) qubits and \(l\) layers, the QUES score, denoted as \(QUES(n,l)\), is determined by experimentally measuring the probability of the ancilla qubit being in the \(\ket{0}\) state at the end of the computation. In the absence of error, the ancilla qubit remains in the \(\ket{0}\) state, indicating that the Hamlitonian evolution is unitary. In [1], \(U_A\) is chosen to be a quantum volume circuit. Drawning \(U_A\) from the haar measure (or an approximation thereof) permits establishing a relationship between the \(QUES(n, l)\) score and the fidelity of the quantum circuit. Notice that the choice of \(U_A\) is free and can be adapted to the quantum chip topology. This procedure is repeated across an ensemble of distinct circuits (approximately 100 different circuits are used in the experimental implementation reported in [1]). Similarly to cross-entropy benchmarking, and owing to the haar-random nature of \(U_A\), the \(n\)-qubits output bitstrings can be utilized to estimate the fidelity of the entire process. Notably, the authors demonstrate that the quantum circuit fidelity can be directly inferred from the value of the \(QUES(n, l)\) score.
Assumptions
- The complexity of the sampling the \(QUES(n,l)\) score relies on the XQUATH assumption [2].
- There is a post-selection for the \(n\)-qubit bitstring \(\{0\}^n\).
- The noise model is assumed to be depolarized (as for many randomized benchmarking protocols).
- The choice of the compilation is free but should be reported.
- The choice of error mitigation method is free but should be reported.
Limitations
- Directly inferring fidelity from \(QUES(n, l)\) values lead to a slightly over-estimated fidelity.
- Limits related to the XQUATH assumption also apply to this method and can make the protocol spoofed [3].
References
- [1]Y. Dong, K. B. Whaley, and L. Lin, “A quantum hamiltonian simulation benchmark,” npj Quantum Information, vol. 8, no. 1, Nov. 2022, doi: 10.1038/s41534-022-00636-x. [Online]. Available at: http://dx.doi.org/10.1038/s41534-022-00636-x
- [2]S. Aaronson and S. Gunn, “On the classical hardness of spoofing linear cross-entropy benchmarking,” arXiv preprint arXiv:1910.12085, 2019.
- [3]X. Gao, M. Kalinowski, C.-N. Chou, M. D. Lukin, B. Barak, and S. Choi, “Limitations of linear cross-entropy as a measure for quantum advantage,” PRX Quantum, vol. 5, no. 1, p. 010334, 2024.