Quantum echoes - Out-of-time-order correlator (OTOC)

Motivation

The Google quantum echoes experiment aims to measure the second-order Out-of-Time-Order Correlator \(\text{OTOC}^{(2)}\). This supremacy experiment goes beyond the XEB protocol used by Google in 2018, which was mainly limited by the verifiability of the quantum computer’s results. The \(\text{OTOC}^{(2)}\) protocol defines a sampling task that is conjectured to be difficult for classical computers, where the results produced by the quantum computer can be verified efficiently.

Protocol

The protocol \(\text{OTOC}^{(2)}\) was proposed by the Google team in 2025 in [1] and summarized in a two-page paper in [2]. The main idea of this protocol is to prepare a single-qubit \(q_\mathrm{m}\) in an eigenstate of a Pauli operator used as the final observable. For example, if the final observable is \(Z\), the qubit could be initialized in \(\ket{0}\), the \(+1\) eigenstate of \(Z\). The quantum chip then evolves according to a randomly picked unitary \(U\) (forward evolution) composed of \(t\) cycles. The entanglement of the qubits on the quantum computer grows as \(t\) grows. Then a small perturbation \(B\) is triggered on a distant qubit \(q_b\) from \(q_m\) (For example, this can be a bit flip \(X\)). The unitary is then run backward, with the \(U^\dagger\) unitary followed by the measuring operator \(M\). For the \(\text{OTOC}^{(2)}\), this protocol is repeated twice:

The following picture represents the quantum circuit associated with the \(\text{OTOC}^{(2)}\) protocol. The qubit \(q_\mathrm{b}\) is fixed during the whole experiment. The experiment is repeated for all the possible locations of \(q_\mathrm{m}\) to build the heatmaps represented on the right of the figure. \(\overline{C}^{(4)}\) corresponds to the expectation value of the qubit \(q_\mathrm{m}\) averaged over several simulations with different random unitaries \(U\). \(\sigma[C^{(4)}]\) corresponds to the standard deviation of \(C^{(4)}\) over the different simulations. If the number of cycles \(t\) is too small, the perturbation \(B\) does not have any effect on the measured qubit \(q_\mathrm{m}\) (see the yellow light cone and black color on the lattice of qubits). As \(t\) increases, distant qubits \(q_\mathrm{m}\) will be gradually impacted by the dissipation of \(B\). The wavefront of the dissipated perturbation exhibits strong variations depending on the structure of the random unitary \(U\).

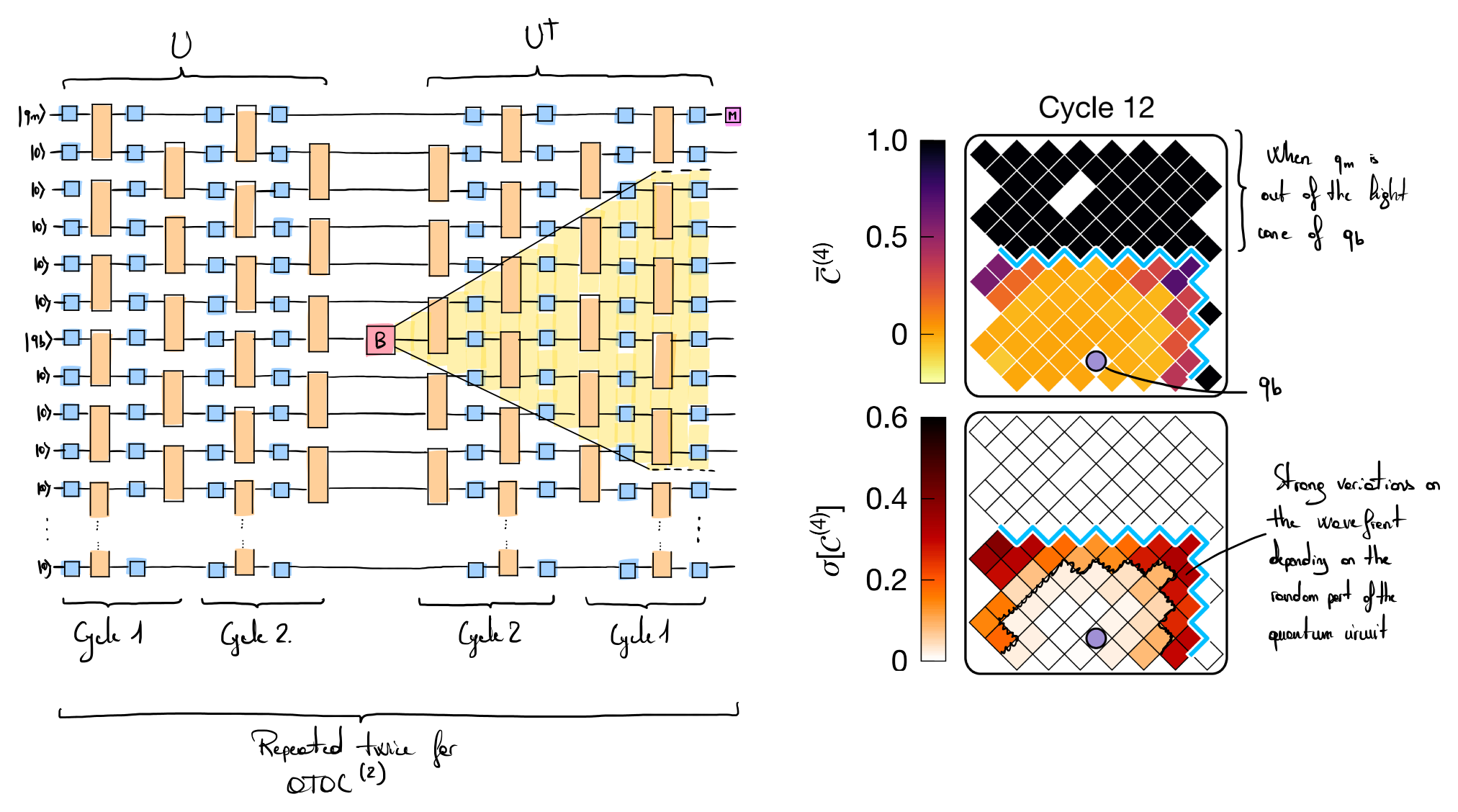
The evaluation of the expectation value \(C^{(4)}\) of each location of \(q_\mathrm{m}\) is conjectured to be difficult to estimate using a classical computer due to the interference patterns that are generated by \(B\) followed by the random unitary \(U^{\dagger}\) that propagate the perturbation. Another interresting property is that the expectation value of \(q_\mathrm{m}\) is highly dependent on the gates composing the random unitary \(U\), which leads to different results depending on the structure of \(U\) (this can be seen with the large value of the standard deviation of the wavefront in Fig 2.b of [1]). The supremacy experiment consists in sampling the value \(C^{(4)}\) faster than any classical method within an additive error \(\epsilon\).

Results

The supremacy claim in [1] has been realised using 65 qubits with a number of cycles \(t=23\). Instead of a single qubit \(q_\mathrm{b}\), three qubits are selected in which \(X\) perturbations are introduced. The final quantity computed in \(C^{(4)}_\mathrm{diag}\), a quantity more complex than \(C^{(4)}\) (see end of part \textit{Large-loop interference in OTOC} for details in [1]). The quantum experiment was performed with 50 different random circuits U and simulated on a quantum computer in approximately 4 days. This experiment has been estimated to require more than 100 years on a classical computer (with a quantum speedup of approximately 13,000).

Implementations

The experiment implementation can be downloaded from the following links: data and code.

References

1. [1]D. A. Abanin et al., “Observation of constructive interference at the edge of quantum ergodicity,” Nature, vol. 646, no. 8086, pp. 825–830, Oct. 2025, doi: 10.1038/s41586-025-09526-6. Available at: http://dx.doi.org/10.1038/s41586-025-09526-6
2. [2]R. King et al., “A simplified version of the quantum OTOC problem,” arXiv preprint arXiv:2510.19751, 2025.