Phase decoherence time \(T2\)

Motivation

A qubit may suffer from phase decoherence due to energy relaxation (already characterized by measuring \(T_1\)) and pure dephasing, which leads to a loss of information concerning the precise phase of the qubit. The effect of this type of noise can be represented on the Bloch sphere by shrinking the state vector to the center of the sphere (representing a decay toward a mixed state). This information loss is characterized by: \(T_\mathrm{2R}\) (usually denoted \(T_2^*\)), measured with the Ramsey experiment, and \(T_\mathrm{2H}\), measured with Hahn echo experiment. Both experiments yield a different \(T_2\) value. The presence of pure dephasing is observed when \(T_2 > 2 T_1\).

Protocol for measuring \(T_\mathrm{2R}\)

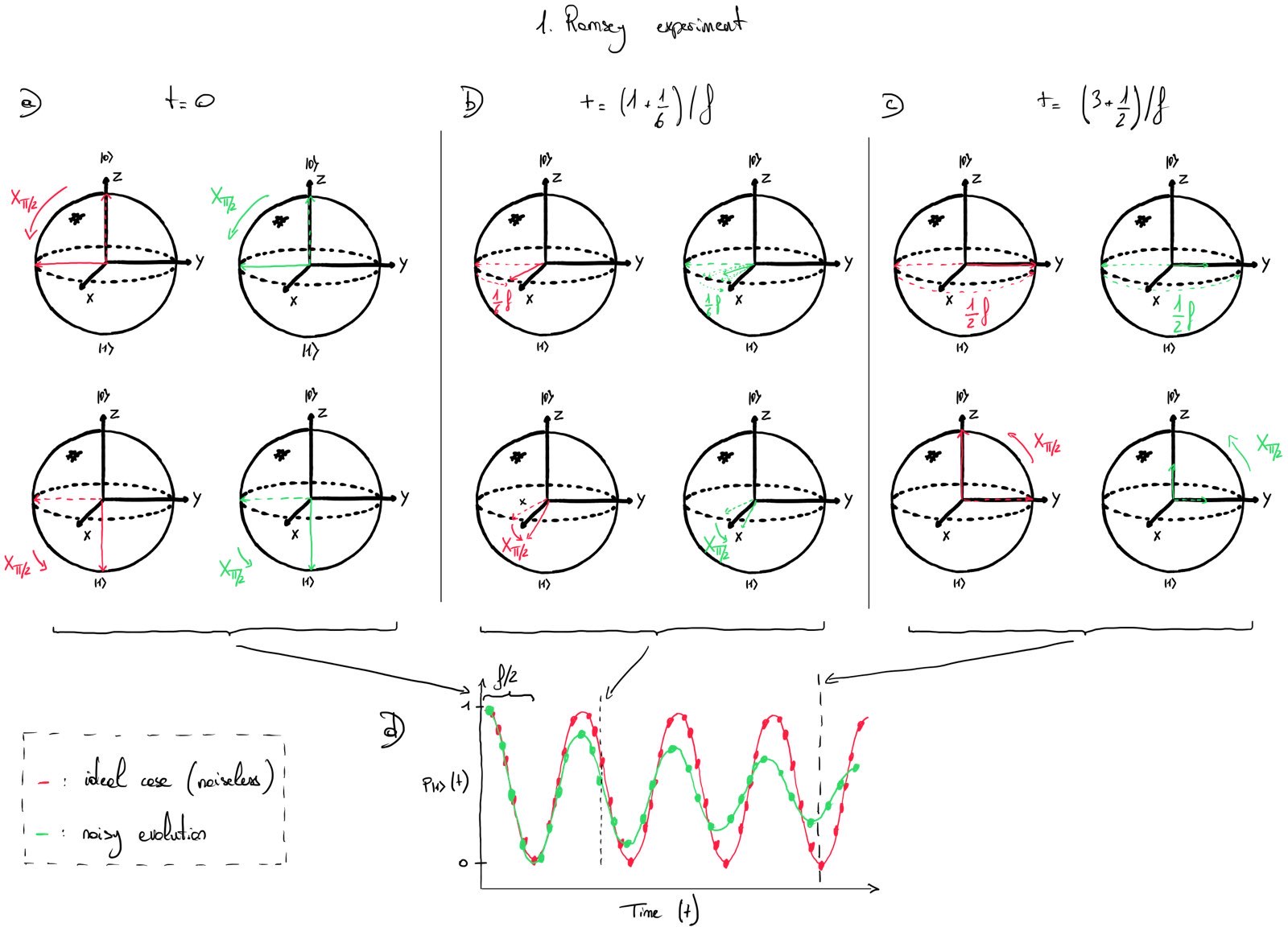
Ramsey spectroscopy aims to measure the phase decoherence time \(T_\mathrm{2R}\) (\(T_2^*\)). This experiment consists of preparing a qubit in state \(\ket{0}\), and applying an \(X_{\pi/2}\) gate. The qubit is then allowed to dephase along the equator of the Bloch sphere (at a frequency \(f\)) during a time \(t\), followed by another \(X_{\pi/2}\) gate. The qubit is then finally measured in the \(Z\)-basis. Fig. 1.a, b, and c show these steps on the Bloch sphere for three different values of \(t\). Vectors in red show the ideal quantum state, while green vectors represent noisy quantum states with errors accumulating with \(t\). The information loss about the phase is illustrated by the green vector shrinking to the sphere’s center.
This experiment is done several times for different values of \(t\). In a perfect experiment without noise, the probability of obtaining the qubit in state \(\ket{1}\) given by \(p_{\ket{1}}(t)\) follows a sinusoid as shown in Fig. 1.d (see the red curve).
The sinusoidal curve decays when the qubit suffers from decoherence effects (see green curve in Fig. 1.d). This sinusoid can be fitted with the following function to extract the value of \(T_\mathrm{2R}\):

\[p_\ket{1}(t) = A e^{-t/T_\mathrm{2R}} \cos \left( 2 \pi ft + \phi \right) + B\]

with \(f\) the frequency of the qubit, \(\phi\) the offset of the cosine, \(A\) the amplitude of the decaying cosine, and \(B\) the baseline offset.

Protocol for measuring \(T_\mathrm{2H}\)

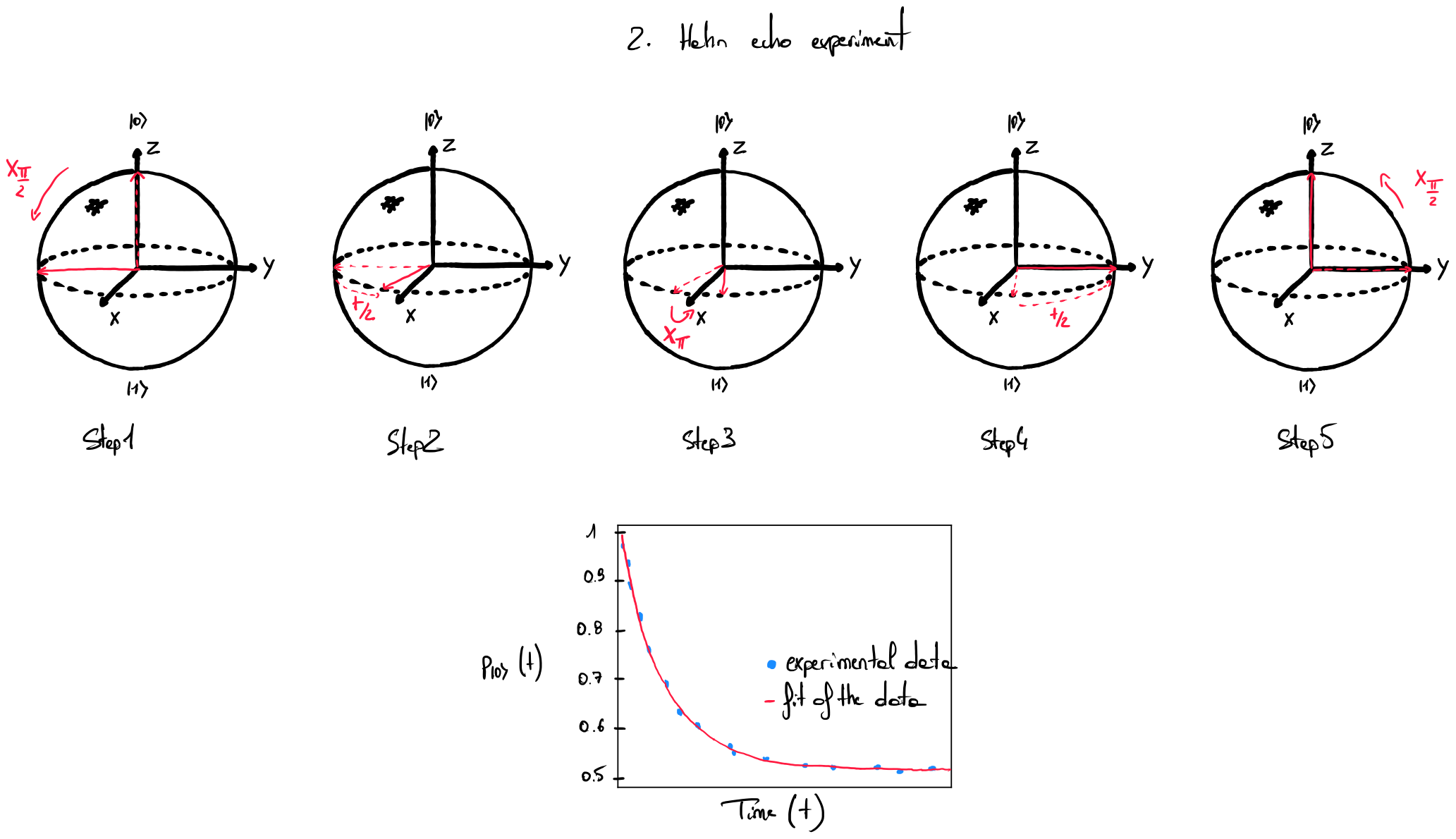
The protocol for measuring the time \(T_\mathrm{2H}\) is slightly different and is based on the Hahn echo experiment [1]. It consists in preparing the qubit in state \(\ket{0}\) followed an \(X_{\pi/2}\) gate (see Step 1 of Fig. 2), and then allowing the qubit to dephase during \(t/2\) time (see Step 2 of Fig. 2). An \(X_\pi\) gate is then applied (see Step 3 of Fig. 2) and the qubit is then again allowed to dephase during \(t/2\) time (see Step 4 of Fig. 2). Finally, an \(X_{\pi/2}\) gate is applied to the qubit. The qubit is then measured in the \(Z\)-basis. In a noiseless scenario, the measurement should always give the state \(\ket{0}\).
However, due to decoherence, the probability of measuring \(\ket{0}\) decays exponentially (see the plot in Fig. 2), and the value of \(T_\mathrm{2H}\) can be extracted by fitting the function:

\[p_\ket{0}(t) = A e^{-t/T_\mathrm{2H}} + B\]

where \(A\) represents the amplitude and \(B\) the offset. In general, \(T_\mathrm{2H} > T_\mathrm{2R}\) because \(T_\mathrm{2R}\) is more sensitive to low frequency noise.

Assumptions

It is assumed that the user has precise knowledge about the duration of each quantum gate and can perform intentional detuning (rotation of the qubit along the equator of the Bloch sphere).

Limitations

Some uncertainty can arise from the measurement of \(T_\mathrm{2R}\) and \(T_\mathrm{2H}\) due to miscalibration of quantum gates and measurements.
As for the \(T_1\) figure of merit, measuring \(T_\mathrm{2R}\) and \(T_\mathrm{2H}\) on quantum annealers can be misleading, essentially because quantum annealers can operate successfully beyond this timescale (see [2] and [3] for interesting discussions on this subject).

Implementation Examples

A tutorial for measuring \(T_\mathrm{2R}\) (\(T_2^*\)) can be found on the QCMet software repository.
Another tutorial for measuring \(T_\mathrm{2R}\) can be found on the qiskit-community github.
A tutorial for measuring \(T_\mathrm{2H}\) can be found on the qiskit-community github.

References

[1]E. L. Hahn, “Spin Echoes,” Physical Review, vol. 80, no. 4, pp. 580–594, Nov. 1950, doi: 10.1103/physrev.80.580. [Online]. Available at: http://dx.doi.org/10.1103/PhysRev.80.580
[2]D. Lall et al., “A review and collection of metrics and benchmarks for quantum computers: definitions, methodologies and software,” arXiv preprint arXiv:2502.06717, 2025.
[3]N. G. Dickson et al., “Thermally assisted quantum annealing of a 16-qubit problem,” Nature Communications, vol. 4, no. 1, May 2013, doi: 10.1038/ncomms2920. [Online]. Available at: http://dx.doi.org/10.1038/ncomms2920