Interleaved Randomized Benchmarking (IRB)

Motivation

The Interleaved Randomized Benchmarking (IRB) protocol was proposed in 2012 by E. Magesan et al. [1] after the multi-qubit Clifford Randomized Benchmarking protocol. The IRB aims to evaluate the average error rate of individual Clifford gates, which was impossible with the multi-qubit CRB method (which evaluates the average error rate of a Clifford group).

Protocol

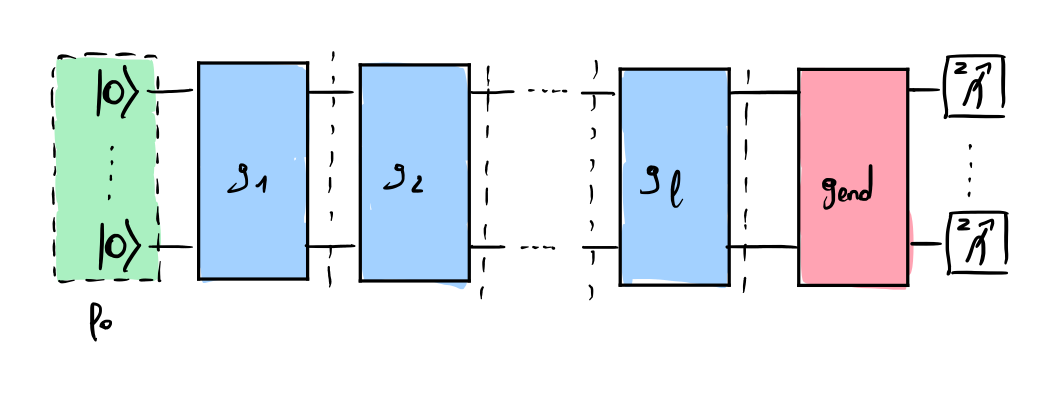
The protocol consists of two experiments. The first experiment involves running a multi-qubit CRB to extract the decay parameter \(\alpha_\mathrm{crb}\) and the corresponding Error Per Clifford \(r_\mathrm{crb}\). The following figure recalls the circuit corresponding to the multi-qubit CRB protocol:

The second experiment aims to evaluate the error rate of the n-qubit Clifford gate of interest \(G\). The gate \(G\) is interleaved with the random \(n\)-qubit Clifford gates \(g_1\) up to \(g_l\). The final gate \(g_\mathrm{end}\) aims to reverse the complete sequence of gates.

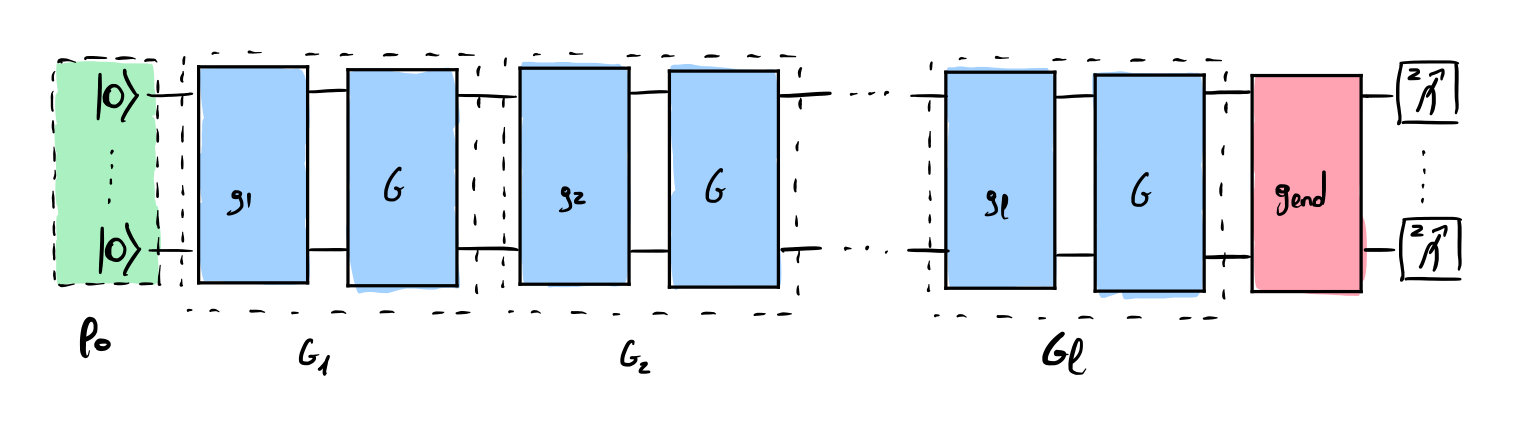
This second experiment aims to extract the decay parameter \(\alpha_\mathrm{irb}\) and the corresponding error rate \(r_\mathrm{irb}\). In practise, \(\alpha_\mathrm{irb}\) should decay faster than \(\alpha_\mathrm{crb}\) due to the additional inserted gates \(G\). The infidelity \(r_\mathrm{G}\) of the gate \(G\) is then estimated with the following approximation:

This method also extracts bounds on the true error rate of G (see equation 5 of [1]).

Assumptions

• This protocol relies on the same assumptions of the multi-qubit CRB protocol (i.e., noise should be depolarizing and Markovian).
• The noise variation between the Clifford gates \(g_i\) should be small. Bounds on the error rate can be estimated (see Step 3 of the protocol in [1]).

Limitations

• This protocol inherits from the same limitations of the multi-qubit CRB protocol (as depth scaling and dependence on compilation strategies).
• As mentioned in [2] and [3], the errors associated with the gate \(G\) can coherently add or cancel with the errors of the Clifford gate, leading to unreliable estimation of the gate fidelity in some cases. It can lead to large differences between the measured error rate \(r_\mathrm{G}\) and the true error rate \(\epsilon_\mathrm{G}\) associated with the gate \(r_\mathrm{G}\).
• It has been shown in [3] that the fidelity estimation is inaccurate when the interleaved gate has a much lower error rate than the average error rate of the Clifford gates.

Extensions

The IRB protocol has been extended to other gates that are not from the Clifford group (see [4] for the evaluation of the T gate and [5] for the assessment of the control-phase gate).

Implementation

A tutorial for implementing IRB is available in the QCMet software repository.
An implementation of the IRB protocol developed by IQM is available in their Benchmark suite.
Another implementation is available in the pyGSTi library.

References

1. [1]E. Magesan et al., “Efficient measurement of quantum gate error by interleaved randomized benchmarking,” Physical review letters, vol. 109, no. 8, p. 080505, 2012.
2. [2]A. Hashim et al., “Practical Introduction to Benchmarking and Characterization of Quantum Computers,” PRX Quantum, vol. 6, no. 3. APS, p. 030202, 2025.
3. [3]J. M. Epstein, A. W. Cross, E. Magesan, and J. M. Gambetta, “Investigating the limits of randomized benchmarking protocols,” Physical Review A, vol. 89, no. 6, p. 062321, 2014.
4. [4]R. Harper and S. T. Flammia, “Estimating the fidelity of T gates using standard interleaved randomized benchmarking,” Quantum Science and Technology, vol. 2, no. 1, p. 015008, 2017.
5. [5]S. Garion et al., “Experimental implementation of non-Clifford interleaved randomized benchmarking with a controlled-S gate,” Physical Review Research, vol. 3, no. 1, Mar. 2021, doi: 10.1103/physrevresearch.3.013204. [Online]. Available at: http://dx.doi.org/10.1103/PhysRevResearch.3.013204