Error Per Layered Gate Protocol (EPLG)

Motivation

This protocol was proposed by IBM in 2023 as a supplement to the quantum volume protocol [1]. Contrary to the quantum volume that focuses on the best-performing subset of qubits on the quantum chip, the Error Per Layered Gate (EPLG) protocol aims to evaluate the performance of a whole quantum computer chip. It also permits the extraction of lower bounds on 2-qubit error rates.

Protocol

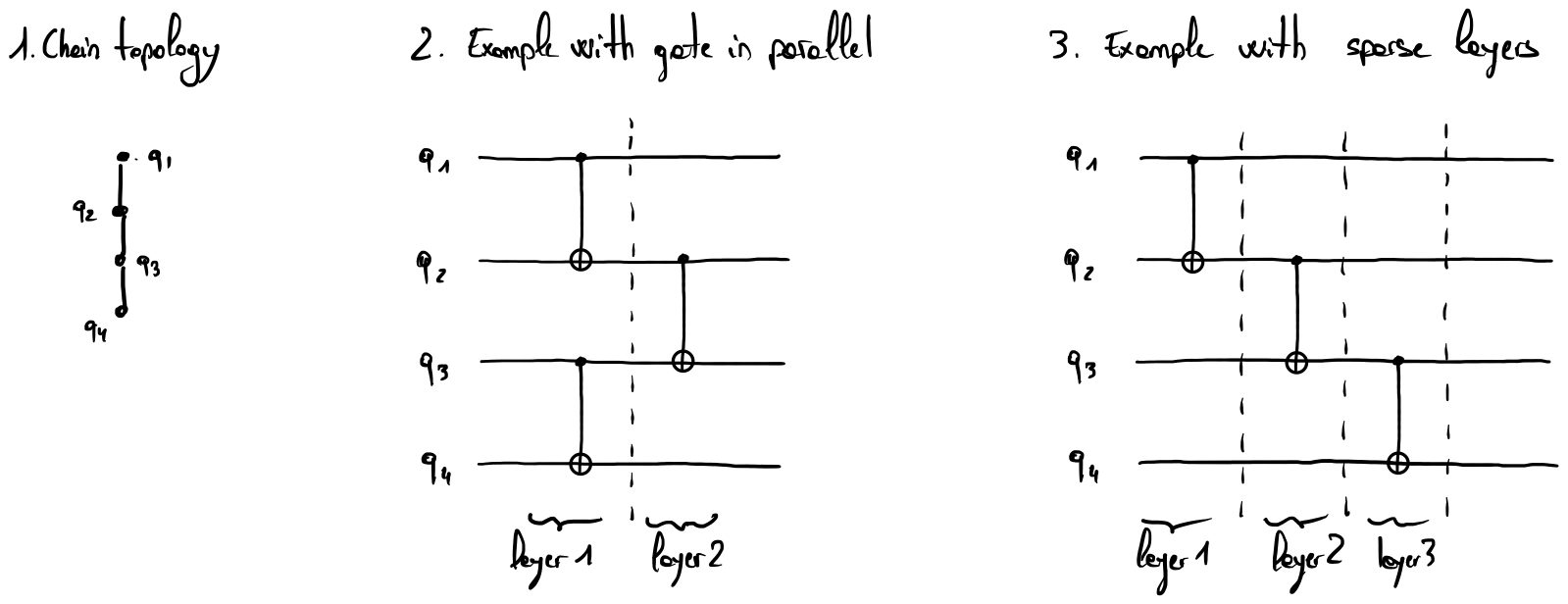
The protocol consists in selecting \(n\) qubits from the quantum chip used to implement an interconnection pattern using two-qubit gates (e.g., CNOT, SWAP, CZ, etc.). For example, Fig. 1 shows a chain pattern with two possible implementations of disjoint layers composed of 2-qubit gates (see Fig.2 and Fig. 3). Fig. 2 implements the chain pattern in two distinct layers, whereas Fig. 3 implements it in three distinct layers.

An implementation is chosen (the implementation of Fig. 2 is selected in the following). A Direct Simultaneous Randomized Benchmarking (combination of Direct Randomized Benchmarking and Simultaneous Randomized Benchmarking) is run for each layer (see Fig. 4). The corresponding circuits are composed of \(l\) blocks with an ending gate \(g_\mathrm{end}\) inverting the previous sequence of quantum gates. Each block \(g_j\) comprises a wall of random Clifford single-qubit gates (yellow squares) and a depth-1 layer of CNOT gates, separated by barriers enforced when running the quantum algorithm.

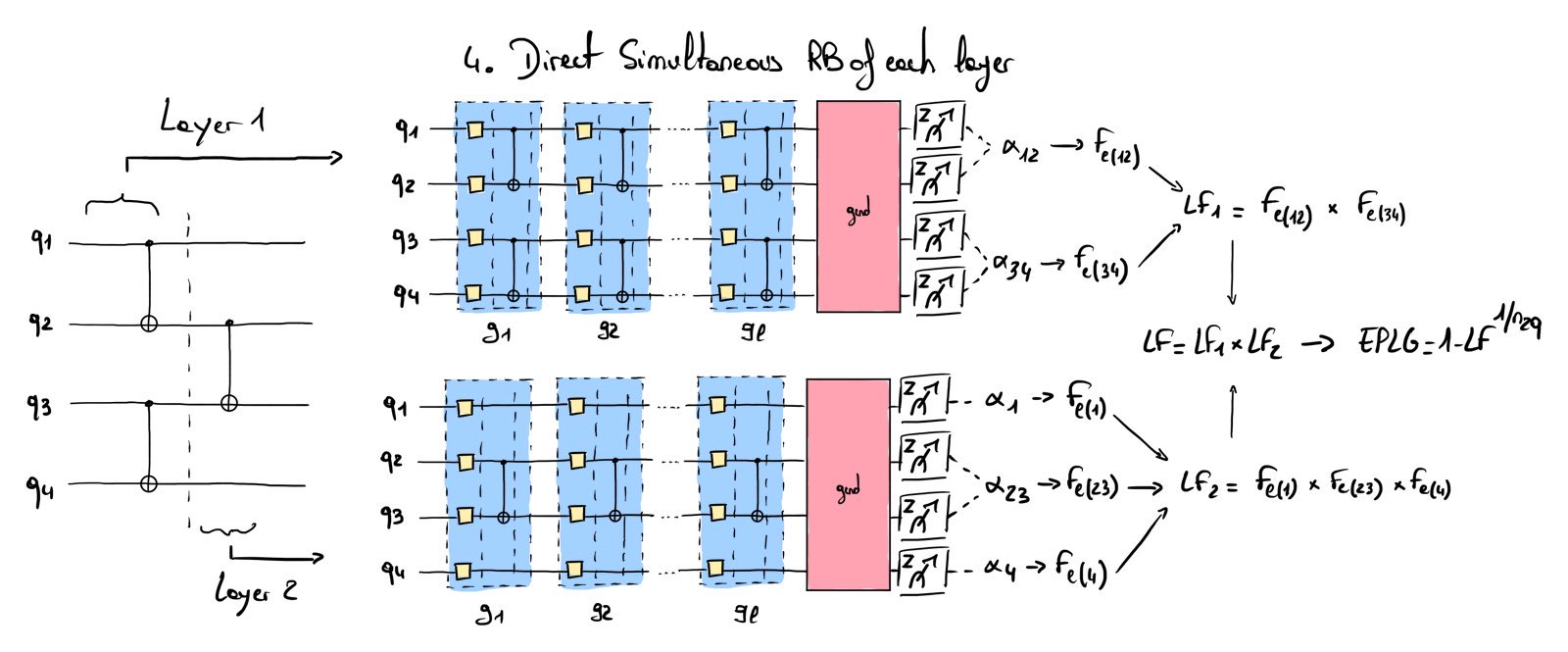
The RB protocol permits the extraction of the exponential decay factors \(\alpha_i\) by fitting the exponential decay function:

where A and B are the coefficients absorbing the errors related to state preparation and measurement. The entanglement fidelity \(F_{e(i)}\) is then computed from each \(\alpha_i\):

where \(d\) is the dimension of the Hilbert space (\(2^n\) for \(n\) qubits). The disjoint layer fidelity \(LF_m\) is a product of each fidelity \(F_i\), and the final layer fidelity \(LF\) is the product of each disjoint layer fidelity. The EPLG is then computed as:

where \(n_{2q}\) corresponds to the number of 2-qubit gates in all the layers (three in the example above).

As the number of qubits grows, the number of possible implementations for a selected pattern grows exponentially. The authors of [1] employ a heuristic to select the best implementation that produces the highest EPLG score (only the best EPLG score is reported).

Assumptions

• The equation that computes the disjoint layer fidelity \(LF_m\) is only valid if there are no cross-talk errors.
• The expression defining \(LF\) represents a lower bound on the error rate and is only a good approximation if the error is low (see Appendix D of [1]).
• This protocol uses the same assumptions as the simultaneous RB protocol (for instance, it considers a Markovian noise).

Limitations

• This protocol relies on simultaneous RB and possesses the same limitations.
• This estimation is just a lower bound on the error rate and has to be cautiously interpreted, as it does not reliably account for crosstalk errors. The EPLG score does not reflect crosstalk error improvements as shown in [2].
• The performance of the final computation strongly depends on the heuristic used to find good patterns that produce high EPLG.
• As shown in subsequent literature [2], the EPLG score does not always align with the algorithm’s performance, especially for large-scale systems.

Implementation

An implementation of the EPLG protocol is made available by the qiskit benchmark community here.

References

1. [1]D. C. McKay, I. Hincks, E. J. Pritchett, M. Carroll, L. C. G. Govia, and S. T. Merkel, “Benchmarking quantum processor performance at scale,” arXiv preprint arXiv:2311.05933, 2023.
2. [2]J. A. Montanez-Barrera, K. Michielsen, and D. E. B. Neira, “Evaluating the performance of quantum processing units at large width and depth.” 2025.